Effect of Earth’s Magnetic Field on Wave Propagation

1. The average magnetic field of the earth is about 40 A/m. The earth’s magnetic field causes the electrons to trace complicated trajectories with cyclotron or gyrofrequency f_g = l.4 MHz at H = 40 A/m.

2. The earth’s magnetic field (B) exerts a deflecting force on the moving electrons. The magnitude of this force on each electron is given by

F = e(v × B)                                – (1)

Where,

e = charge of electron (C)

F = force on the electron in the ionosphere whose charge is e (N)

v = velocity of the electron, m/s

B = magnetic flux density (Wb/m²) = μ_oH

H = magnetic field intensity of earth (A/m).

• This exerted force is always perpendicular to the velocity of electron and magnetic field of the earth.
• Thus, whenever radio wave enters into the ionosphere, a component of magnetic field which is perpendicular to the electric field of the incident radio waves cause oscillating electrons to follow an elliptical path.
• When the frequency of skywave becomes equal to the natural frequency of revolution of free electrons due to resonance, the energy of radio waves is absorbed by the revolving electrons and they follow a spiral path. The frequency at which this phenomenon occurs is known as gyro or cyclotron frequency.

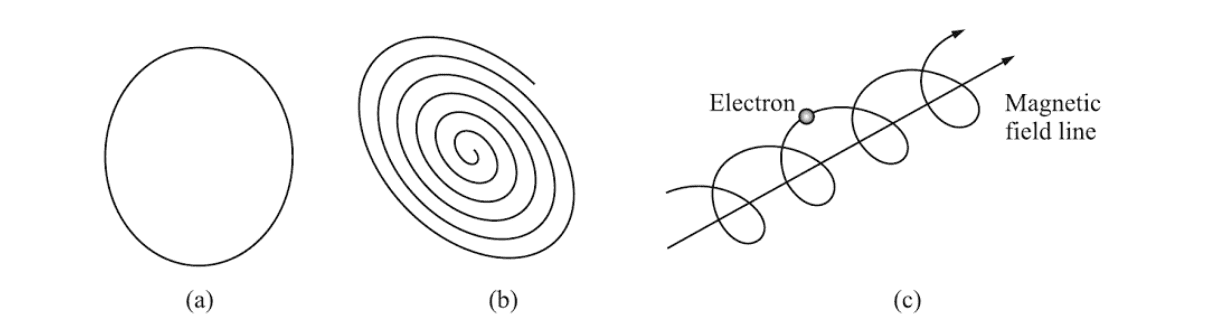
3. Gyro or Cyclotron Frequency: It is defined as the lowest natural frequency of a wave at which charged particles spiral in a fixed magnetic field.

It is a vector quantity and mathematically defined as:

f_g = (1/2π)(eB/m) = (1/2π)(μ_oeH/m)                             -(2)

Where,

e = charge of electron (C)

B = magnetic flux density (Wb/m²)

m = mass of the particle (kg)

μ_o = permeability of ionosphere (H/m)

H = magnetic field intensity (A/m)

Putting,

e = 1.6 x 10^–19 C

m = 9.1 x 10^–31 kg

B = 5 x 10^–5 Wb/m²

We get cyclotron or gyro frequency f_g = l.4 MHz

• If the frequency of sky wave is less than gyro frequency, electrons move in helical path.
• If the frequency of sky wave is greater than gyrofrequency, electrons move in an elliptical path.

PROOF:

Assume that electron revolves in a circular path of radius r due to the perpendicular magnetic field of the earth. Hence necessary centripetal force is provided by Lorentz force.

F_m = (mv²)/r                         -(3)

Equating equation (1) and (3), we get

v/r = eB/m

Since v/r = ω = 2πf

Therefore,

f = (1/2π)(eB/m) = (1/2π)(μ_oeH/m)                                  -(4)

Equation (4) gives the expression of gyro frequency.