Image Restoration and Image Degradation Model

Image restoration is the process of recovering an image that has been degraded by some knowledge of degradation function H and the additive noise term ${{\eta}(x,y)}$ . Thus in restoration, degradation is modelled and its inverse process is applied to recover the original image.

Objective of image restoration:

The objective of image restoration is to obtain an estimate of the original image ${{f}(x,y)}$ . Here, by some knowledge of H and ${{\eta}(x,y)}$ , we find the appropriate restoration filters, so that output image ${\widehat{f}(x,y)}$ is as close as original image ${{f}(x,y)}$ as possible since it is practically not possible (or very difficult) to completely (or exactly) restore the original image.

Terminology:

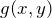${g(x,y)}$ = degraded image
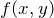${f(x,y)}$ = input or original image
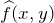${\widehat{f}(x,y)}$ = recovered or restored image
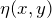${{\eta}(x,y)}$ = additive noise term

In spatial domain:

${g(x,y) = h(x,y) \circledast f(x,y) + \eta(x,y)}$

where, ${\circledast}$ represents convolution

In frequency domain:

After taking fourier transform of the above equation:

${G(u,v) = H(u,v)F(u,v) + N(u,v)}$

If the restoration filter applied is ${R(u,v)}$ , then

${\widehat{F}(u,v) = R(u,v)[G(u,v)]}$

${\widehat{F}(u,v) = R(u,v)H(u,v)F(u,v) + R(u,v)N(u,v)}$

${\widehat{F}(u,v) \approx F(u,v)}$ (for restoration)

as restoration filter ${R(u,v)}$ is the reverse of degration function ${H(u,v)}$ and neglecting the noise term. Here, ${H(u,v)}$ is linear and position invariant.

Image Restoration and Image Degradation Model

Objective of image restoration:

In spatial domain:

In frequency domain:

Leave a Comment Cancel Reply

Interested in Knowledge

Archives